Actualités
Voir toutes les actualitésVincent L. Pecoraro is an invited professor at ENS in April 2024.
Candidatures ouvertes jusqu'au 23 avril 2024
New IMAP paper on scalable & cost-effective MOF for CO2 capture
Merci à l'ENS Lyon et bravo aux 1As pour le TFChim
En route pour le Tournoi Francais des Chimistes: 22-23 Mars à Lyon
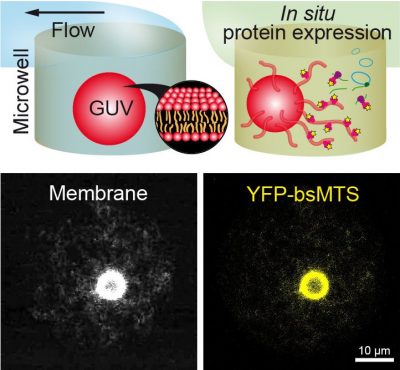
Sedimentation-Based Confinement of Individual Giant Unilamellar Vesicles in Microchamber Arrays with a Dynamically Exchangeable Outer Medium
Recherche et formation
 |
 |
 |
 |
Suivez-nous
| Tweets by Chimie__ENS |